A matemática por trás de um dos principais algoritmos de Machine Learning
Machine Learning (ML), ou Aprendizado de Máquina, é um termo do momento. O mundo está passando por grandes transformações, mudando de forma rápida e brusca. Coisas inimagináveis há 5 ou 10 anos atrás são corriqueiras nos dias de hoje.
Grande parte dessa mudança veio por causa do ML. Mas não se engane, os algoritmos de ML são antigos, uma vez que são teoremas estatísticos utilizados de forma automática. O ingrediente que faltava para que essa explosão ocorresse era o Big Data – mas não iremos falar sobre isso, deixaremos para um próximo post.
O que quero trazer para vocês aqui é uma visão de como o aprendizado de máquina funciona, mostrar que não é mágica, é simplesmente matemática com uma boa dose de alto processamento (computação).
Hoje, irei falar para vocês sobre Regressão Linear (simples e múltipla), um dos algoritmos de ML mais utilizados. No decorrer deste post, irei mostrar como a parte matemática funciona.
Introdução
O que é:
Em estatística, Regressão Linear é uma equação para se estimar o valor de uma variável y, dados os valores de outras variáveis x’s. Ou seja, busca-se uma relação entre as variáveis que possa ser representada como uma função linear. Caso não seja uma função linear, devemos procurar por modelos de regressão não-linear.
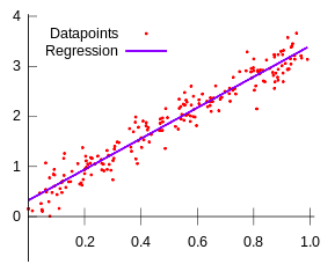
Figura 1: exemplo de regressão linear.
Elas são usadas para o Aprendizado de Máquina Supervisionado, ou seja, o Dataset utilizado contém várias variáveis de entradas e apenas 1 variável de resposta (target).
Dentro de Aprendizado Supervisionado, os algoritmos podem ser de dois tipos: Classificação, onde o objetivo é mapear as variáveis de entrada em categorias discretas; e Regressão, capaz de mapear variáveis de entrada para alguma função contínua.
Notações:
A notação $x^{i}$ representa os valores de entrada (‘input’ ou variáveis de entrada) e $y^{i}$ representa o valor que se quer prever (‘output’ ou variável target). Os exemplos (training set) sempre serão escritos da seguinte forma: ($x^{i}$, $y^{i}$) tal que $1\leq i\leq m$. Portanto, o i é o índice no training set e m é a quantidade de dados que existe. Já o X representa o conjunto dos valores inputs, a mesma lógica vale para Y em relação ao valores outputs.
Em alguns casos, haverá mais de uma variável de entrada. Assim, para representar cada coluna, usaremos seu número subscrito no x: $x_{j}^{i}$, sendo que o $1\leq i\leq m$ e $1\leq j\leq n$. Onde m representa a quantidade de exemplos e n representa a quantidade de variáveis de entrada.
Hipótese:
Basicamente, o Aprendizado Supervisionado tem como objetivo, dado um training set, aprender uma função h: $X\rightarrow Y$, onde h(x) será um bom preditor para y. Por diversas razões, chamamos essa função h de Hipótese.
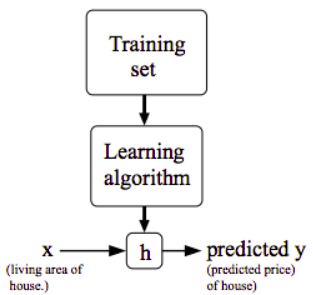
Figura 2: Representação gráfica da função h.
Cost Function
Para mensurar o quão precisa esta nossa função de hipótese, utilizamos a Cost Function: $J(\Theta) = \frac{1}{2m}*\sum_{i=1}^{m}(h_{\Theta}( x^{(i)})-y^{(i)})^{2}$
Nosso objetivo é achar os melhores parâmetros $\Theta$, tal que $J(\Theta)$ seja o menor possível.
Forma Matricial:
Uma importante e interessante forma de pensar nessas funções é na sua forma matricial. Não se engane, ao traduzir essas equações da linguagem natural para linguagem de programação, não devemos utilizar o comando for demasiadamente, uma vez que seu gasto computacional é muito grande, já que utilizamos grandes datasets. Por isso, sempre colocamos os X, Y e os thetas, em vetores/matrizes. Assim, utilizamos a multiplicação de matrizes ao nosso favor, reduzindo o tempo e o custo computacional gasto.
Linguagens como MATLAB e Octave, assim como a biblioteca NumPy do Python foram criadas com intuito de facilitar esse tipo de operação.
Regressão Linear Simples
Sempre que houver apenas 1 variável de entrada e 1 variável de resposta usaremos esse tipo de regressão.
Hipótese:
Como já explicado acima, usaremos a Função de Hipótese para criar a linha de regressão igual mostrado na Figura 1. A função h é definida como: $h_{\Theta} = \Theta_{0} + \Theta_{1}* x$. Veja, essa equação sempre criará uma reta, sendo $\Theta_{0}$ o coeficiente linear e o $\Theta_{1}$ o coeficiente angular.
Cost Function:
Já a função de custo é definida da seguinte forma: $J(\Theta_{0}, \Theta_{1}) = \frac{1}{2m} * \sum_{i=1}^{m}(h_{\Theta}(x^{(i)})-y^{(i)})^{2}$
Regressão Linear Múltipla
Sempre que houver apenas n variáveis de entrada e 1 variável de resposta usaremos esse tipo de regressão.
Hipótese:
É definida da seguinte forma: $h_{\Theta}(X) = \Theta_{0} + \Theta_{1}x_{1}^{(i)} + \Theta_{2}x_{2}^{(i)} + … + \Theta_{n}x_{n}^{(i)}$
Observa-se que a quantidade de parâmetros theta depende da quantidade de x’s.
Sua forma matricial é:
$h_{\Theta}(X) = \begin{bmatrix} \Theta_{0} & \Theta_{1} & … & \Theta_{n} \end{bmatrix} \begin{bmatrix} x_{0}\\ x_{1}\\…\\x_{n} \end{bmatrix}= \Theta^{T}x$, onde $x_{0}=1$
Note que não importa quantos thetas ou quantos x’s tem, a multiplicação de matrizes resolve com apenas um comando, por isso, ao codificar, não há necessidade de criar uma função para Regressão Linear Simples e outra para Múltipla.
Cost Function:
Já na função de custo, não há grandes alterações. Ela é definida: $J(\Theta_{0},\Theta_{1},\Theta_{2},…,\Theta_{n}) = J(\Theta^{T}) = \frac{1}{2m} \sum_{i=1}^{m}(h_{\Theta}(x^{(i)})-y^{(i)})^{2}$, onde o T sobrescrito ao theta representa a transposta.
Gradient Descent (GD)
Método para achar os mínimos de J (Cost Function), para isso, devemos já definir os valores de thetas, assim, de forma iterativa, iremos calcular um novo theta.
Algoritmo:
Cria-se um loop, repetindo enquanto converge (costuma-se passar uma quantidade de repetições), segue o pseudo-código:
loop {
$t_{0} = \Theta_{0} - \alpha \frac{\partial}{\partial \Theta_{0}} J$
$t_{1} = \Theta_{1} - \alpha \frac{\partial}{\partial \Theta_{1}} J$
…
$t_{n} = \Theta_{n} - \alpha \frac{\partial}{\partial \Theta_{n}} J$
$\Theta_{0}, \Theta_{1}, …, \Theta_{n} = t_{0}, t_{1}, …, t_{n}$
}
Taxa de Aprendizagem:
Responsável pelo tamanho do passo quando atualizar os thetas, quanto maior for, maior será o passo o que pode ocasionar na perda do mínimo local, quanto menor for, menor o passo e demora mais. Normalmente, comece com passos grandes e vá diminuindo, assim, costuma-se iniciar com \(\\alpha\)=0,05.
Derivadas parciais:
$\frac{\partial}{\partial\Theta_{0}} \frac{1}{2m} \sum_{i=1}^{m} (h_{\Theta}(x^{(i)})-y^{(i)})^{2} = \frac{1}{m}\sum_{i=1}^{m} (h_{\Theta}(x^{(i)})-y^{(i)})$
$\frac{\partial}{\partial\Theta_{j}} \frac{1}{2m} \sum_{i=1}^{m} (h_{\Theta}(x^{(i)})-y^{(i)})^{2} = \frac{1}{m}\sum_{i=1}^{m} (h_{\Theta}(x^{(i)})-y^{(i)}) x_{j}^{(i)}, 1\leq j\leq n$
Feature Normalize:
Para otimizar o algoritmo, podemos colocar os valores de entrada em um intervalo parecido (normalmente entre 0 e 1). Assim, o theta chega mais rápido ao mínimo. Lembre-se, o intervalo não pode ser muito grande nem muito pequeno.
Realize a seguinte operação para fazer a normalização: $novoX^{(i)} = \frac{x^{(i)}-\mu_{1} }{\sigma_{1}}$
Onde, $novoX^{(i)}$ é o novo x, $\sigma_{1}$ é o desvio padrão, $\mu_{1}$ é a média e $x^{(i)}$ é o antigo x.
Normal Equation (NE):
Outro método para achar o mínimo de J, porém este é um método não iterativo, portanto, não deve aplicar Feature Normalize. Seja a seguinte situação:
- m exemplos: $(x^{(1)}, y^{(1)}), …, (x^{(m)}, y^{(m)})$
- n features: $(x_{1}, x_{2}, …, x_{n})$
- n+1 thetas: $(\Theta_{0}, \Theta_{1}, \Theta_{2}, …, \Theta_{n})$
Assim, formamos as seguintes matrizes:
$x^{(i)}=\begin{pmatrix}1\\x_{1}^{(i)}\\…\\x_{n}^{(i)}\end{pmatrix}_{(n+1)\times1}$
$X=\begin{pmatrix}x^{(1)^{T}}\\x^{(2)^{T}}\\…\\x^{(m)^{T}}\end{pmatrix}_{m\times(n+1)}$
$Y=\begin{pmatrix}y^{(1)}\\y^{(2)}\\…\\y^{(m)}\end{pmatrix}_{m\times 1}$
$ \Theta=\begin{pmatrix}\Theta_{0} \\ \Theta_{1}\\…\\ \Theta_{n}\end{pmatrix}_{(n+1)\times 1}$
Logo, para achar o vetor theta faz a seguinte multiplicação de matriz: $\Theta=(X^{T} * X)^{-1} * X^{T} * Y$
GD vs NE:
Acabamos de ver dois métodos para achar o mínimo da Cost Function, mas fica a pergunta, qual deles é melhor? A resposta, como sempre, depende. Abaixo listei algumas características de ambos.
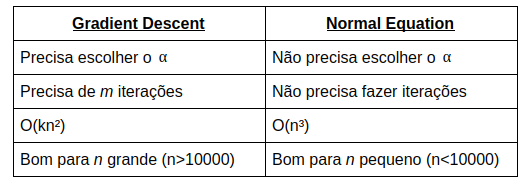
Conclusão:
O que mostrei aqui é apenas a ponta do iceberg. Há inúmeros algoritmos de machine learning com diversos proposta, a única coisa comum entre eles é que, como demonstrado acima, não é mágica, e sim matemática. Caso queira aprender mais sobre, acesse o seguinte curso na Coursera. Nele, você verá mais sobre o que falei, inclusive sobre o funcionamento das redes neurais artificiais.
Bônus:
Caso esteja curioso para saber como ficariam esses algoritmos usando a linguagem de programação Octave, visite o meu repositório.


Comentários